Todo sobres ángulos.

Todo sobres ángulos.

por   1:08 p.m.   2 comentarios:

Ángulos

Un ángulo es la región del plano comprendida entre dos semirrectas con origen común. A las semirrectas se las llama lados y al origen común vértice.

Medición de ángulos

Para medir ángulos utilizamos el grado sexagesimal (°)

Grado sexagesimal es la amplitud del ángulo resultante de dividir la circunferencia en 360 partes iguales.

1º = 60' = 3600''

1' = 60''

Radián

Radián (rad) es la medida del ángulo central de una circunferencia cuya longitud de arco coincide con la longitud de su radio.

1 rad= 57° 17' 44.8''

360º = 2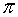rad

Operaciones con ángulos

Suma de ángulos

Gráfica

La suma de dos ángulos es otro ángulo cuya amplitud es la suma de las amplitudes de los dos ángulos iniciales.

Numérica

1º Para sumar ángulos se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos; y se suman.

2º Si los segundos suman más de 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirán a los minutos.

3º Se hace lo mismo para los minutos.

Resta de ángulos

Gráfica

La resta de dos ángulos es otro ángulo cuya amplitud es la diferencia entre la amplitud del ángulo mayor y la del ángulo menor.

Numérica

1º Para restar ángulos se colocan los grados debajo de los grados, los minutos debajo de los minutos y los segundos debajo de los segundos.

2º Se restan los segundos. Caso de que no sea posible, convertimos un minuto del minuendo en 60 segundos y se lo sumamos a los segundos del minuendo. A continuación restamos los segundos.

3º Hacemos lo mismo con los minutos.

Multiplicación de ángulos

Gráfica

La multiplicación de un número por un ángulo es otro ángulo cuya amplitud es la suma de tantos ángulos iguales al dado como indique el número.

Numérica

1º Multiplicamos los segundos, minutos y grados por el número.

2º Si los segundos sobrepasan los 60, se divide dicho número entre 60; el resto serán los segundos y el cociente se añadirán a los minutos.

3º Se hace lo mismo para los minutos.

División de ángulos

Gráfica

La división de un ángulo por un número es hallar otro ángulo tal que multiplicado por ese número da como resultado el ángulo original.

:4 =

Numérica

Dividir 37º 48' 25'' entre 5

1º Se dividen los grados entre el número.

2º El cociente son los grados y el resto, multiplicando por 60, los minutos.

3º Se añaden estos minutos a los que tenemos y se repite el mismo proceso con los minutos.

4º Se añaden estos segundos a los que tenemos y se dividen los segundos.

Tipos de ángulos

Clasificación de ángulos según su medida

Agudo < 90°	Recto = 90°	Obtuso>90°
Convexo < 180°	Llano = 180°	Cóncavo > 180°
Nulo = 0º	Completo = 360°
Negativo < 0º	Mayor de 360°

Tipos de ángulos según su posición

Ángulos consecutivos

Ángulos consecutivos son aquellos que tienen el vértice y un lado común.

Ángulos adyacentes

Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en polongación del otro.

Forman un ángulo llano.

Ángulos opuestos por el vértice

Son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.

Los ángulos 1 y 3 son iguales.

Los ángulos 2 y 4 son iguales.

Clases de ángulos según su suma

Ángulos complementarios

Dos ángulos son complementarios si suman 90°.

Ángulos suplementarios

Dos ángulos son suplementarios si suman 180°.

Ángulos entre paralelas y una recta transversal

Ángulos correspondientes

Los ángulos 1 y 2 son iguales.

Ángulos alternos internos

Los ángulos 2 y 3 son iguales.

Ángulos alternos externos

Los ángulos 1 y 4 son iguales.

Ángulos en la circunferencia

Ángulo central

El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.

La medida de un arco es la de su ángulo central correspondiente.

Ángulo inscrito

El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.

Mide la mitad del arco que abarca.

Ángulo semi-inscrito

El vértice de ángulo semis-inscrito está en la circunferencia, un lado secante y el otro tangente a ella.

Mide la mitad del arco que abarca.

Ángulo interior

Su vértice es interior a la circunferencia y sus lados secantes a ella.

Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.

Ángulo exterior

Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:

Mide la mitad de la diferencia entre las medidas de los arcos que abarcan sus lados sobre la circunferencia.

Ángulos de un polígono regular

Ángulo central de un polígono regular

Es el formado por dos radios consecutivos.

Si n es el número de lados de un polígono:

Ángulo central = 360° : n

Ángulo central del pentágono regular= 360° : 5 = 72º

Ángulo interior de un polígono regular

Es el formado por dos lados consecutivos.

Ángulo interior =180° − Ángulo central

Ángulo interior del pentágono regular = 180° − 72º = 108º

Ángulo exterior de un polígono regular

Es el formado por un lado y la prolongación de un lado consecutivo.

Los ángulos exteriores e interiores son suplementarios, es decir, que suman 180º.

Ángulo exterior = Ángulo central

Ángulo exterior del pentágono regular = 72º

Definición de bisectriz

La bisectriz de un ángulo es la recta que pasando por el vértice del ángulo lo divide en dos ángulos iguales.

Trazar la bisectriz

1º Se traza un arco correspondiente al ángulo

2º Desde los dos extremos del arco trazado se trazan, con cualquier abertura del compás, dos arcos que han de cortarse en un punto.

3º La bisectriz se obtiene dibujando la recta que une ese punto con el vértice.

Otra forma de dibujar la bisectriz de un ángulo

1.Con centro en el vértice del ángulo se traza una circunferencia de cualquier amplitud.

2.Desde los puntos de corte de la circunferencia con los lados del ángulo se trazan dos circunferencias con el mismo radio.

3.La recta que pasa por el vértice del ángulo y uno de los puntos de corte de las circunferencias es la bisectriz.

Incentro

El incentro es el punto de corte de las tres bisetrices de un triángulo.

El incentro es el centro de una circunferencia inscrita en el triángulo.

Leer Mas

Puntos,rectas,segmentos y planos.

Puntos,rectas,segmentos y planos.

por   1:06 p.m.   No hay comentarios.:

Puntos y rectas

Puntos

Un punto no tiene dimensiones.

Sirve para indicar una posición.

Se nombran con letras mayúsculas.

Rectas

Una recta tiene una dimensión: longitud.

Se designan mediante dos de sus puntos o mediante una letra minúscula.

Dos puntos determinan una recta.

Dos rectas que se cortan determinan un punto.

Una recta indica una dirección y dos sentidos contrarios, según se recorra la recta de izquierda a derecha o de derecha izquierda.

Semirrectas

Una semirrecta es cada una de las partes en que queda dividida una recta por uno cualquiera de sus puntos.

Planos

Un plano posee dos dimensiones: longitud y anchura.

Se nombran mediante letras griegas: α (alfa), β (beta)...

Dos planos que se cortan determinan una recta.

Un plano viene determinado por:

Tres puntos no alineados.

Dos rectas que se cortan.

Dos rectas paralelas.

Por un punto y una recta.

Semiplanos

Un semiplano es cada una de las partes en que queda dividido un plano por una cualquiera de sus rectas.

Posiciones relativas de rectas en un plano

Rectas paralelas

Son las que estando en el mismo plano, no son secantes.

Rectas secantes

Son las que se cortan en un único punto, llamado punto de intersección.

Rectas coincidentes

Son aquellas en las que todos sus puntos se superponen.

Rectas perpendiculares

Son dos rectas secantes que dividen un plano en cuatro partes iguales.

Segmentos

Definición de segmento

Segmento es la porción de recta limitada por dos puntos, llamados extremos.

Se designa por los puntos que lo limitan o por una letra minúscula.

Tipos de segmentos

Segmento nulo

Un segmento es nulo cuando sus extremos coinciden.

Segmentos concatenados

Dos segmentos son concatenados cuando tienen un extremo en común.

Segmentos consecutivos

Dos segmentos son consecutivos cuando además de tener un extremo en común pertenecen a la misma recta.

Mediatriz de un segmento

La mediatriz de un segmento es la recta que pasa por el punto medio del segmento y es perpendicular a él.

Operaciones con segmentos

Suma de segmentos

La suma de dos segmentos es otro segmento que tiene por inicio el origen del primer segmento y como final el final del segundo segmento.

La longitud del segmento suma es igual a la suma de las longitudes de los dos segmentos que lo forman.

Resta de segmentos

La resta de dos segmentos es otro segmento que tiene por origen el final del segmento menor y por final el final del segmento mayor.

La longitud del segmento diferencia es igual a la resta de las longitudes de los dos segmentos.

Producto de un número por un segmento

El producto de un número con un segmento es otro segmento resultado de repetir el segmento tantas veces como indica el número por el que se multiplica.

La longitud del segmento obtenido es igual al número por la longitud del segmento inicial.

División de un segmento por un número

La división de un segmento por un número es otro segmento tal que multiplicado por ese número da como resultado el segmento original.

La longitud del segmento obtenido es igual la longitud del segmento inicial divido por el número.

División de un segmento en partes

Dividir el segmento AB en 3 partes iguales.

1. Se dibuja una semirrecta de origen el extremo A del segmento.

2. Tomando como unidad cualquier medida, se señalan en la semirrecta 3 unidades de medida a partir de A.

3. Por cada una de las divisiones de la semirrecta se trazan rectas paralelas al segmento que une B con la última división sobre la semirrecta. Los puntos obtenidos en el segmento AB determinan las 3 partes iguales en que se divide.

Leer Mas

Anteproyecto de Matemática 8vo grado-1er Periodo.

Anteproyecto de Matemática 8vo grado-1er Periodo.

por   11:50 a.m.   No hay comentarios.:

Centro:_____________________
Alumno: ____________________
Fecha: ______________________
Prof. _______________________

І-) Selecciona la respuesta correcta.

1- ) Es una rama de las matemáticas que se ocupa de estudiar las propiedades generales de las operaciones aritméticas y lo números. a-) El álgebra 
b-) la geometría
c-) la aritmética 2- ) Es una combinación de letras, números y signos de operaciones. a-) El álgebra 
b-) la geometría
c-) expresión algebraica  3- ) Es una expresión algebraica que consta de dos o más términos. a-) binomio
b-) polinomio
c-) expresión lineal

ІІ-) Escribe F o V según a quien pertenezca cada número y justifica.

a-)  1.5 no pertenece a N ___, _____________________ b-) √49 no pertenece a Q ____ , ____________________   c-) -3 pertenece a Z ___ , _________________________

ІЦ-) Escribe:

a-) Dos racional entre -1.5 y 0.5 __________  b-) cuatro números racional, dos positivo y dos negativo ___, ___ , ____ c-) Tres números racionales entre 0 y 1 ____, ____, _____

ІV-) Según el enunciado escriba la expresión algebraica.

1- ) La mitad de un número menos La mitad de otro número____ 2- ) La suma de dos números es 2________ 3- ) Cinco veces la edad de Pozo menos la edad de Elena es igual a cien_____

V-) Dada la siguiente tabla, coloque cada número donde le corresponde.

Números	Enteros	Racionales	Irracionales
0.5, -10, 0, 2.333, 44.1, 0.001, 3.14…, 0.12456…, 1/5, 8/4, 0.1, 1.1234567…, 5.5, √2, √4, ∏, 100, 100

VІ-) Reduzca los siguientes términos.

1- ) 7a -10b2 + 6b2 -2a + 9a =
2- ) 8a³ -5b +6b -6a3 -a³ =
3- ) 5x2 -y -2x2 +3y +6x2 =

VІІ-) Identifica las constante y las variables las siguientes expresiones.

1-) 2x³ + 5x – 3
variables________
constantes ______

2-) x2+ 3
variables________
constantes _______

VІІІ-) Dada la expresión algebraica escríbe en enunciado verbal.

1-)    5x – 2y – 7 _____________________________
2-)     x2 + 3y ________________________________

ІX-)  Realice las siguientes operaciones con números racionales.

X-) Parea el numero decimal con la fracción que le corresponde.

XІ-) Resuelva los siguientes problemas con números racionales.

a-) Un trabajador ganó el lunes 2 y 2/3 euros y el martes 9 y 2/5 euros.
¿Cuántos euros ganó en los dos días? b-) Para preparar un pastel, se necesita: 2/3 de un paquete de 750 g de azúcar, 3/5


de un paquete de harina de kilo, 3/5 de una barra de mantequilla de 200 g. ¿Qué cantidades en gramo se necesitan para preparar el pastel? c-) Una familia ha consumido en un día de verano, dos botellas de litro y medio


de agua, 4 botes y un 1/3 de litro de zumo. ¿Cuántos litros de líquido han bebido?

XІІ-) Halla el valor numérico de las siguientes expresiones.
1- )    x2+ 3y               x=4      y=5
2- )   4ab + b2 − 3      a=3      b=4

XІІІ-) Resuelva los siguientes problemas.

1- )  Un números más diecisiete es igual a cuarenta. ¿Cuál es ese número?  

2- ) En una caja hay el doble de caramelos de menta que de fresa y el triple de 

caramelos de naranja que de menta y fresa juntos. Si en total hay 144 caramelos,

 ¿cuántos hay de cada sabor?

XІV-) Resuelva las siguientes ecuaciones de 1er grado.

a-) x + 10 = 13  

 b-)  3x -4 = x + 8                

c-) 40x = 120

 b-)  2(5x -4) -7 = x + 8

XV-) Responda las siguientes preguntas y justifica

1- ) Los triángulos 2, 3, 4 y 5 han sido obtenidos a partir del triángulo 1.

¿Cuál de ellos corresponde a la traslación del triángulo 1?

a) triángulo 2       b) triángulo 3      c) triángulo 4     d) triángulo 5    e) Ninguno

¿En cuál de los siguientes casos se representa mejor una reflexión según la recta dada?

3- ) El Tetris es un video juego inventado en 1984, en el cual se deben aplicar repetidas veces transformaciones geométricas a figuras diferentes para encajar. Considerando la jugada que aparece a la derecha, ¿qué transformaciones geométricas debes realizar para hacer encajar Correctamente la figura 1 en A?, ¿y para encajar la figura 2 en B?

4-) Según las figuras, que tipos de transformación geométricas representan

XVІ-) Área y Perímetro: Haga lo que se le pide en cada caso. 1- ) Dados los puntos A(-1,-1) B(-1,3) C(2,-1) construya la figura y halla el perímetro y el área.

2-) Dados los puntos  M(1,-1)   B(5,-1)  C(1,-3)  C(5,-3) construya la figura y halla el perímetro y el área.

XVII-) Transformaciones Geométricas: Haga lo que se le pide en cada 

caso. 
1- ) Dados los puntos Q(1,-1)   B(5,-1)  R(1,-3)  C(5,-3) construya la figura y reflejarla con respecto al eje X.

2-) Dados los puntos  M(1,1)   B(4,1)  C(1,3)  R(4,3) M(2,4)   N(3,4)   construya la figura y refléjela con respecto al eje Y

3- ) Dados los puntos Q(1,-1)   B(5,-1)  R(1,-3)  C(5,-3) construya la figura y hágala rotar a 90 grado.

4-) Dados los puntos M(1,1) B(4,1) C(1,3) R(4,3) M(2,4) N(3,4) construya la figura y hágala rotar a 90 grado.

5- ) Dados los puntos Q(1,-1) B(5,-1) R(1,-3) C(5,-3) construya la figura y trasládela 2 unidades hacia abajo.

6-) Dados los puntos M(1,1) B(4,1) C(1,3) R(4,3) M(2,4) N(3,4) construya la figura y trasládela 3 unidades hacia la izquierda y dos hacia abajo.

Leer Mas