Conjuntos numéricos
Los conjuntos numéricos con los que has trabajado tanto en Enseñanza Básica como en Enseñanza Media, se van ampliando a medida que se necesita resolver ciertas problemáticas de la vida diaria.
Números naturales (IN)
Los primeros números que el hombre inventó fueron los números naturales, los cuales se utilizaban y aún se utilizan para contar elementos de un conjunto. Los números naturales sirven para contar y ordenar fundamentalmente.
El nombre “Números Naturales” seguramente surge debido a que estos números son los que aparecen por primera vez en el proceso natural de contar o enumerar los objetos de un conjunto.
Los números naturales son un conjunto de números de la forma: 1, 2, 3,…. que denotaremos con el símbolo IN, esto es:
Números naturales (IN)
Los primeros números que el hombre inventó fueron los números naturales, los cuales se utilizaban y aún se utilizan para contar elementos de un conjunto. Los números naturales sirven para contar y ordenar fundamentalmente.
El nombre “Números Naturales” seguramente surge debido a que estos números son los que aparecen por primera vez en el proceso natural de contar o enumerar los objetos de un conjunto.
Los números naturales son un conjunto de números de la forma: 1, 2, 3,…. que denotaremos con el símbolo IN, esto es:
IN = {1, 2, 3, 4, 5 ...}
Si al conjunto de los números naturales se le une el número cero, este nuevo conjunto se denota con el símbolo IN0, esto es,
IN0 = {0, 1, 2, 3 ...}.
Es posible establecer una correspondencia entre los números naturales y los puntos de una recta (recta numérica) de la siguiente manera.
Dada una recta, se selecciona un punto arbitrario de ésta para representar el cero (0) y otro punto a la derecha del cero para representar el uno (1), a este segmento le llamamos segmento unidad. Luego dividimos toda la recta en segmentos que tengan la misma longitud que el segmento unidad, para así representar los números 1, 2, 3, 4,... (en este orden) que se encontrarán a la derecha del cero.
En una recta numérica el punto que representa el cero recibe el nombre de origen.
Dada una recta, se selecciona un punto arbitrario de ésta para representar el cero (0) y otro punto a la derecha del cero para representar el uno (1), a este segmento le llamamos segmento unidad. Luego dividimos toda la recta en segmentos que tengan la misma longitud que el segmento unidad, para así representar los números 1, 2, 3, 4,... (en este orden) que se encontrarán a la derecha del cero.
En una recta numérica el punto que representa el cero recibe el nombre de origen.
Una representación gráfica de IN0 en la recta numérica se muestra en la figura 1:
Figura 1. IN0 en la recta numérica.
De IN y IN0 se pueden formar variados subconjuntos, entre ellos se encuentran:
• El Conjunto de los números pares es un subconjunto de IN0 donde:
{x Є IN0 / x=2n, n Є IN0 } = {0, 2, 4, 6, 8, 10,....}.
• El Conjunto de los números impares es un subconjunto de IN0 donde:
{x Є IN0 / x=2n + 1, n Є IN0 } ={1, 3, 5, 7, 9, 11,....}.
Observa que estos dos conjuntos no tienen elementos en común y que si se unen ambos, forman el conjunto IN0
• El conjunto de los Múltiplos de un número es un subconjunto de IN donde:
Se llaman múltiplos de un número a todos los números que resultan de la multiplicación de ese número con cada uno de los naturales. Los múltiplos de un número n pertenecen al conjunto formado por:
{1·n, 2·n, 3·n, 4·n,...}.
• El Conjunto de los números pares es un subconjunto de IN0 donde:
{x Є IN0 / x=2n, n Є IN0 } = {0, 2, 4, 6, 8, 10,....}.
• El Conjunto de los números impares es un subconjunto de IN0 donde:
{x Є IN0 / x=2n + 1, n Є IN0 } ={1, 3, 5, 7, 9, 11,....}.
Observa que estos dos conjuntos no tienen elementos en común y que si se unen ambos, forman el conjunto IN0
• El conjunto de los Múltiplos de un número es un subconjunto de IN donde:
Se llaman múltiplos de un número a todos los números que resultan de la multiplicación de ese número con cada uno de los naturales. Los múltiplos de un número n pertenecen al conjunto formado por:
{1·n, 2·n, 3·n, 4·n,...}.
• El conjunto de los Divisores de un número es un subconjunto de IN donde:
Llamamos divisores de un número, a todo el conjunto de números que lo divide exactamente.
• El Conjunto de los Números Primos es un subconjunto de IN donde:
El número natural p>1 es un número primo si sus únicos divisores son 1 y p.
Algunos números primos son:
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29,...}.
Llamamos divisores de un número, a todo el conjunto de números que lo divide exactamente.
• El Conjunto de los Números Primos es un subconjunto de IN donde:
El número natural p>1 es un número primo si sus únicos divisores son 1 y p.
Algunos números primos son:
{2, 3, 5, 7, 11, 13, 17, 19, 23, 29,...}.
1.2. Números enteros (Z)
Si se requiere dar solución a la sustracción 4 – 9, es necesario encontrar un número que sumado a 9 de cómo resultado 4. Este número no existe en IN0.
Para que la sustracción tenga siempre solución, se extiende la recta numérica hacia la izquierda, de modo que a cada punto que representa un número natural le corresponde un punto simétrico a él, ubicado a la izquierda del cero.
Si se requiere dar solución a la sustracción 4 – 9, es necesario encontrar un número que sumado a 9 de cómo resultado 4. Este número no existe en IN0.
Para que la sustracción tenga siempre solución, se extiende la recta numérica hacia la izquierda, de modo que a cada punto que representa un número natural le corresponde un punto simétrico a él, ubicado a la izquierda del cero.
Cada uno de estos nuevos puntos ubicados a la izquierda de la recta numérica, respecto al cero, representa un número negativo.
Entonces, el conjunto de los números enteros es la unión del conjunto de los números naturales, el cero y los números negativos. Este conjunto se denota por Z, donde:
Entonces, el conjunto de los números enteros es la unión del conjunto de los números naturales, el cero y los números negativos. Este conjunto se denota por Z, donde:
Z={..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}
Una representación gráfica de en la recta numérica se muestra en la figura 2:
__|____|____|____|___|____|____|____|____|____|____|__
...-5 -4 -3 -2 -1 0 1 2 3 4 5...
...-5 -4 -3 -2 -1 0 1 2 3 4 5...
Figura 2. Z en la recta numérica.
Cada número negativo es considerado el opuesto o inverso aditivo de su simétrico positivo y, cada número positivo, es el opuesto de su simétrico negativo. Por ejemplo, 3 es el opuesto o inverso aditivo de -3.
La distancia que existe entre un número a y el cero la representaremos a través del valor absoluto y se expresará como |a|. Como se refiere a una distancia, el valor absoluto de un número siempre es positivo.
La distancia que existe entre un número a y el cero la representaremos a través del valor absoluto y se expresará como |a|. Como se refiere a una distancia, el valor absoluto de un número siempre es positivo.
Por ejemplo, la distancia entre 15 y 0 en la recta numérica es de 15 unidades, entonces |15| = 15.
Ahora, las distancia entre -15 y 0, también es de 15 unidades en la recta numérica, luego |−15| = 15.
Ahora que conocemos los números enteros, podemos utilizarlos para representar situaciones como:
o Seis grados bajo cero (-6 ºC)
o Una deuda de tres mil pesos ($ -3.000)
Ahora que conocemos los números enteros, podemos utilizarlos para representar situaciones como:
o Seis grados bajo cero (-6 ºC)
o Una deuda de tres mil pesos ($ -3.000)
1.2.1. Regularidades numéricas
Al realizar ciertas operaciones aritméticas entre los números enteros, es posible encontrar propiedades que resultan curiosas e interesantes por presentarse como patrones o regularidades numéricas.
Estas regularidades son sucesiones de números que forman un conjunto que siguen cierta regla de formación. La sucesión la denotaremos por {an}, con n Є IN donde an es el término general de la sucesión. Por lo tanto, se entenderá por sucesión una colección de números dispuestos uno a continuación de otro.
Al realizar ciertas operaciones aritméticas entre los números enteros, es posible encontrar propiedades que resultan curiosas e interesantes por presentarse como patrones o regularidades numéricas.
Estas regularidades son sucesiones de números que forman un conjunto que siguen cierta regla de formación. La sucesión la denotaremos por {an}, con n Є IN donde an es el término general de la sucesión. Por lo tanto, se entenderá por sucesión una colección de números dispuestos uno a continuación de otro.
El término general de una sucesión es una fórmula que permite conocer el valor de un determinado término si se conoce previamente el lugar que ocupa en la misma. Por costumbre, al término general de una sucesión se le denota por an y se hablará de término n-ésimo.
Ejemplos de sucesiones son:
Ejemplos de sucesiones son:
Números racionales (Q)
Si tratamos de resolver una ecuación como 3x=7, sólo conociendo el conjunto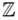
, nos damos cuenta que carecemos de dicha solución. Debido a esto, se ha hecho necesario encontrar un conjunto que “extienda” a 
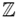. Dicho conjunto está formado por los números racionales que denotaremos por 
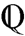, y que se definen de la siguiente forma:
Si tratamos de resolver una ecuación como 3x=7, sólo conociendo el conjunto
, nos damos cuenta que carecemos de dicha solución. Debido a esto, se ha hecho necesario encontrar un conjunto que “extienda” a . Dicho conjunto está formado por los números racionales que denotaremos por , y que se definen de la siguiente forma:
Decimos que a es un número racional, si es posible expresarlo de la forma a=p/q, donde p, q Є Z y q ≠ 0.
De esta forma
De esta forma
Donde, p es llamado numerador y q es el denominador de la fracción.
El conjunto de los racionales es denso porque entre dos números racionales siempre podemos encontrar otro número racional.
Ejemplos:
- Generalmente, los resultados fraccionarios de diferentes problemas se deben expresar con el denominador en forma natural (entero positivo distinto de cero).
El conjunto de los racionales es denso porque entre dos números racionales siempre podemos encontrar otro número racional.
Ejemplos:
- Generalmente, los resultados fraccionarios de diferentes problemas se deben expresar con el denominador en forma natural (entero positivo distinto de cero).
- Los números enteros se pueden expresar como fracción con denominador 1, por lo tanto, todo número entero es también un número racional:
Sea a/b Є Q; se conviene en representar los números racionales preferentemente por medio de fracciones en las cuales el denominador es un número entero positivo.
Recordemos además, que si aЄZ, bЄZ, b>0,el número racional a/b se puede considerar como el cociente que se obtiene al dividir a por b; en donde b indica el número de partes en que se divide la unidad y a el número de partes que se toman de esta división.
De esta manera, si se divide en dos partes iguales cada segmento unidad en la recta numérica, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente.
Recordemos además, que si aЄZ, bЄZ, b>0,el número racional a/b se puede considerar como el cociente que se obtiene al dividir a por b; en donde b indica el número de partes en que se divide la unidad y a el número de partes que se toman de esta división.
De esta manera, si se divide en dos partes iguales cada segmento unidad en la recta numérica, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 2, como se muestra en el ejemplo siguiente.
De igual manera, si se divide en tres partes iguales cada segmento unidad en la recta, podemos representar los números racionales cuya representación fraccionaria tiene como denominador 3, como se muestra en el ejemplo siguiente.
Representación decimal de un número racional:
Toda fracción puede expresarse como decimal dividiendo el numerador por el denominador.
Un número decimal finito es un número racional que puede ser representado por una fracción decimal.
Ejemplo:
0,25 es un número racional ya que 1/4=0,25, pues:
1 : 4 = 0, 25
-0/ 10
- 8/20
- 20/0
Un número decimal finito es un número racional que puede ser representado por una fracción decimal.
Ejemplo:
0,25 es un número racional ya que 1/4=0,25, pues:
1 : 4 = 0, 25
-0/ 10
- 8/20
- 20/0
Los números decimales periódicos o semiperiódicos también son números racionales ya que pueden ser escritos como fracciones. Observemos:
Ejemplos:
El número decimal periódico es un número racional puesto que .
El número decimal semiperiódico es un número racional ya que
Ejemplos:
El número decimal periódico es un número racional puesto que .
El número decimal semiperiódico es un número racional ya que
1.3.3. Transformación de un número decimal finito a una fracción decimal:
Para realizar este proceso basta con escribir una fracción cuyo numerador se conforme por el número completo sin la coma decimal, y que el denominador sea una potencia de 10 que tiene tantos ceros como cifras tiene la parte decimal, es decir, tantos ceros como la cantidad de cifras después de la coma. Observemos un ejemplo:
Ejemplo:
Para realizar este proceso basta con escribir una fracción cuyo numerador se conforme por el número completo sin la coma decimal, y que el denominador sea una potencia de 10 que tiene tantos ceros como cifras tiene la parte decimal, es decir, tantos ceros como la cantidad de cifras después de la coma. Observemos un ejemplo:
Ejemplo:
Transformación de un número decimal periódico o semiperiódico a una fracción decimal:
Todo número decimal periódico o semiperiódico puede convertirse en una fracción. A través de un ejemplo veamos cómo realizar este proceso.
Ejemplo:
Orden en Q:
Dados dos números racionales a/b · c/d siempre se cumplirá sólo uno de los tres casos:
I. Los números a/b · c/d son iguales si se cumple que a·d=b·c
II. El número a/b es mayor que c/d si se cumple que a·d>b·c
III. El número a/b es menor que c/d si se cumple que a·d
Dados dos números racionales a/b · c/d siempre se cumplirá sólo uno de los tres casos:
I. Los números a/b · c/d son iguales si se cumple que a·d=b·c
II. El número a/b es mayor que c/d si se cumple que a·d>b·c
III. El número a/b es menor que c/d si se cumple que a·d
Operatoria en Q:
En cursos anteriores conociste la forma de operar con números fraccionarios. Ahora que conocemos la relación existente entre una fracción y un número racional, definiremos las cuatro operaciones básicas entre números racionales expresados como fracciones.
Adición de números racionales:
En cursos anteriores conociste la forma de operar con números fraccionarios. Ahora que conocemos la relación existente entre una fracción y un número racional, definiremos las cuatro operaciones básicas entre números racionales expresados como fracciones.
Adición de números racionales:
Dados dos números racionales a/b y c/d, se define la suma entre ellos como:
a/b + c/d = a·d + b·c/b·d
1.3.6.2. Sustracción de números racionales:
Dados dos números racionales a/b y c/d, se define la sustracción entre ellos como:
a/b - c/d = a·d - b·c/b·d
1.3.6.3. Multiplicación de números racionales:
Dados dos números racionales a/b y c/d, se define la multiplicación entre ellos como:
a/b · c/d = a·c/b·d
División de números racionales:
Dados dos números racionales a/b y c/d, se define la división entre ellos como:
Dados dos números racionales a/b y c/d, se define la división entre ellos como:
a/b : c/d = a/d · d/c, donde d/c es el inverso multiplicativo de c/d
1.4. Números irracionales (Q’)
Un número irracional es un decimal infinito, cuya parte decimal no posee periodo, es decir, no puede ser representado como racional.
Ejemplos:
Un número irracional es un decimal infinito, cuya parte decimal no posee periodo, es decir, no puede ser representado como racional.
Ejemplos:
Todas las raíces inexactas son números irracionales.
Como los números irracionales no pueden ser representados como cuocientes de números enteros (ya que no son racionales), no es posible escribir explícitamente su forma decimal, pero sí tienen la importante propiedad de poder ser aproximados con el grado de precisión que se necesite.
Como los números irracionales no pueden ser representados como cuocientes de números enteros (ya que no son racionales), no es posible escribir explícitamente su forma decimal, pero sí tienen la importante propiedad de poder ser aproximados con el grado de precisión que se necesite.
La resta y el producto de números irracionales puede no ser un número irracional.
Por Ejemplo:
Por Ejemplo:
Números reales (R)
El conjunto de los números reales se denota por la letra IR y está conformado por la unión del conjunto de los números racionales con el conjunto de los números irracionales:
El conjunto de los números reales se denota por la letra IR y está conformado por la unión del conjunto de los números racionales con el conjunto de los números irracionales:
Figura 3. Reresentación gráfica de los conjuntos numéricos
Responderemos lo mas rápido posible.