Los Cuartiles dividen a un conjunto de datos de tal manera que,
Q1: es el valor antes del cual quedan un
25% de los datos;
Q2: Es idéntico a la mediana, los datos quedan en un
50%, y
Q3: los datos quedan en un 75%, que es el tercer cuartil.
El proceso para localizar cuartiles es semejante al que se utiliza para encontrar la mediana.
1) Ordene los “n” datos desde el menor al mayor.
2) Esta es la fórmula para determinar cualquier cuartil: k(n+1) /4
Siendo “k” igual al cuartil buscado y “n” al número de datos.
Nota: Si la posición cae entre dos enteros, deberá emplear la formula…
Qk= E1 + (E2-E1)e
E1=número donde está el cuartil.
E2= numero que le sigue donde está el cuartil.
e=parte decimal de la posición.
Ejemplo:
1-) Determinar el 3er cuartil de los siguientes datos: 1, 2, 8, 8, 9, 7, 4, 8, 9.
Ordenamos los datos de menor a mayor: 1, 2, 4, 7, 8, 8, 8, 9, 9.
Luego buscamos la formula.

Donde.
K= 3 (cuartil buscado)
N= 9 (total de datos)
Entonces:

Como el resultado es un número decimal “7.5”, la posición 7 y 8.

El cuartil # 3, será:
Q3=8 + (9-8)(0.5)
Q3= 8 + 1(0.5)
Q3= 8 + 0.5 = 8.5
Deciles Dk:
Los deciles se localizan en la muestra de modo que un 20 % de los datos son menores o iguales que el segundo decil, D2; un 80 % de los datos son menores o iguales al octavo decil, D8, y un 90 % de los datos menores o iguales que el noveno decil, D5:

Para calcular los deciles y percentiles utilizamos el mismo procedimiento de los cuartiles, pero con la siguientes formulas:
Siendo “k” igual al decil buscado y “n” al número de datos.
Nota: En ambos casos, si la posición cae a la mitad entre dos enteros, deberá tomarse como cuartil la media de ambos enteros.
Ejemplo:
Determinar el 7mo decil y el 25 percentil de los siguientes datos: 1, 2, 8, 8, 9, 7, 4, 8, 9.
Ordenamos los datos de menor a mayor: 1, 2, 4, 7, 8, 8, 8, 9, 9.
Luego buscamos la formula.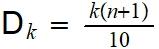
Donde.
K= 7 (decil buscado)
N= 9 (total de datos)
Entonces:
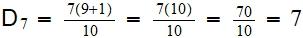
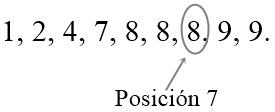
El decil # 7, será: 8.
AQUÍ NO SE APLICA LA FORMULA PASADO, YA QUE, NO EL CUARTIL RECAE EN UN NÚMERO.
El percentiles:

Donde.
K= 25 (percentil buscado)
N= 9 (total de datos)
Ordenamos los datos de menor a mayor: 1, 2, 4, 7, 8, 8, 8, 9, 9.
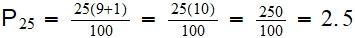
P25 = 2 + (4-2) (0.5)
P25 = 2 + (2) (0.5)
P25= 2 + 1 = 3
VER VÍDEO EJEMPLO.
Actividad de Aprendizaje.
I-) Analiza y haz lo que te piden en cada ejercicio.
1-) Una maquinaria registra las siguientes temperaturas en un período de producción de 20 días.
42°, 53°, 39°, 33°, 40°, 41°, 50°, 35°, 28°, 29°, 37°,
43°, 34°, 31°, 44°, 57°, 32°, 45°, 46°, 48°.
Determinar la posición de los valores que corresponda al Q4, Q2, D6, P7:
2-) Los datos siguientes corresponden a los tiempos de reacción de una muestra de 33 sujetos, medidos en centésimas de segundo: 55, 51, 60, 56, 64, 56, 63, 63, 61, 57, 62, 50, 49, 70, 72, 54, 48, 53, 58, 66, 68, 45, 74,
65, 58, 61, 62, 59, 64, 57, 63, 52, 67.
Calcule la media, el primer y el tercer cuartil, directamente a partir de los datos.
3-) Hemos medido la variable neuroticismo en un grupo de sujetos obteniendo los siguientes resultados: 3, 5, 3, 6, 4, 2, 8, 3, 7, 5, 8, 9, 4, 5, 5, 3
Calcule moda, mediana y el percentil 35.
4-) Un experimento, medido en grados ¿emigrados, arroja los siguientes resultados: 28, 31, 28, 30. 28. 27, 30. 32, 35, 26, 25, 29, 26, 28, 25. 31, 31, 32, 27, 30, 31, 31, 25, 28
Hallar los percentiles P18, P70 y dar su respectiva Interpretación:



























