Área Lateral de un Tronco de Cono (cono truncado).
Área lateral de un Tronco de cono
Un tronco de cono o cono truncado es el cuerpo geométrico que se obtiene al cortar un cono mediante un plano paralelo a su base y eliminar la parte que contiene su cúspide. El siguiente cuerpo es un cono recto truncado:
Partes de un tronco de un cono.
En el tronco de cono se forma un trapecio, entre: la altura (h), los
A= π (r² + R²)
Para determinar el área lateral, utilizamos la siguiente formula.
Para determinar el área total, solo sumamos el resultado de las dos fórmulas anterior.
Ejemplo:
Calcular el área lateral del siguiente tronco de cono.
Aquí buscamos la formula del área lateral y luego sustituimos los valores que nos dan el tronco.
En la figura se ve como se forma un triángulo rectángulo, donde “g” es la hipotenusa, por tal razón buscaremos a “g” de la siguiente manera.
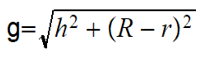
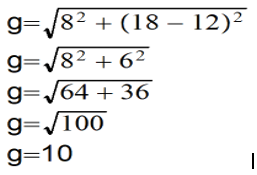
Ahora que ya tenemos el valor de “g”, procedemos a realizar el ejercicio.
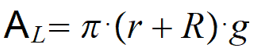
Ejemplo # 3:
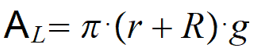
Entonces sustituimos los valores en la fórmula.
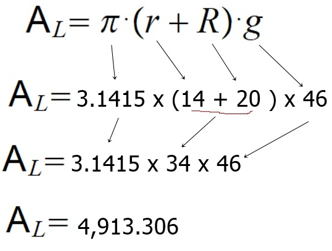
Entonces sustituimos los valores en la fórmula.Ahora, como queremos comprar papel decorativo y debemos saber los centímetros cuadrados que pediremos en la tienda, para eso debemos sacarle la raíz cuadrada

1-) En el parque municipal de la comunidad se van a colocar baldes de basura y se tiene el siguiente modelo como se muestra en la figura. El alcalde desea saber que cantidad de material se invertirá en cada balde para su construcción. Según las medidas que se muestran a continuación. Determinar la cantidad de material que se gastará por unidad.
2-) Una banda de músicos ha adquirido una tambora, instrumentos de percusión de forma de cono truncado, cuyas dimensiones son de 40 centímetros de alto por 26 centímetros de diámetro superior y 8 centímetros de diámetro en la boca inferior. ¿Cuántos centímetros cuadrados de tela con diseños serán necesarios para cubrir el contorno de dicha tambora? Considerar = 3,14.
Un tronco de cono o cono truncado es el cuerpo geométrico que se obtiene al cortar un cono mediante un plano paralelo a su base y eliminar la parte que contiene su cúspide. El siguiente cuerpo es un cono recto truncado:
radios (r, R) y la generatriz (g).
Para determinar el área de las dos bases, utilizamos la siguiente formula.
Para determinar el área de las dos bases, utilizamos la siguiente formula.
A= π (r² + R²)
Para determinar el área lateral, utilizamos la siguiente formula.
Para determinar el área total, solo sumamos el resultado de las dos fórmulas anterior.
Ejemplo:
Aquí buscamos la formula del área lateral y luego sustituimos los valores que nos dan el tronco.
Ejemplo # 2:
Calcular el área lateral del siguiente tronco de cono.
Buscamos la formula.
Luego:
Π = 3.1415
r = 12
R= 18
g = ?
En este caso nos faltaría el valor de “g”. Buscamos a “g” de la siguiente manera.
h = 8
R-r= 18-12=6
Ahora que ya tenemos el valor de “g”, procedemos a realizar el ejercicio.
Luego:
Π = 3.1415
r = 12
R= 18
g = 10
Ejemplo # 3:
Aplicación del Tronco de un Cono.
1-) Tengo una lámpara identifica a la que se muestra en la figura, pero en mal estado, si decido forrar la parte superior de la lámpara, y sabiendo que la parte diagonal (generatriz) de la lámpara mide 46 cm, el diámetro superior 28 cm (r=D/2) y el diámetro inferior 40cm (R=D/2) ¿Qué cantidad de papel decorativo necesitaré?
1-) Tengo una lámpara identifica a la que se muestra en la figura, pero en mal estado, si decido forrar la parte superior de la lámpara, y sabiendo que la parte diagonal (generatriz) de la lámpara mide 46 cm, el diámetro superior 28 cm (r=D/2) y el diámetro inferior 40cm (R=D/2) ¿Qué cantidad de papel decorativo necesitaré?
Luego:
Π = 3.1415
r = D/2 = 28/2 = 14
R= D/2 = 40/2 = 20
g = 46
Entonces sustituimos los valores en la fórmula.Ahora, como queremos comprar papel decorativo y debemos saber los centímetros cuadrados que pediremos en la tienda, para eso debemos sacarle la raíz cuadrada
a “4, 913.306”

Entonces, la cantidad de papel que pediremos será igual a:
Ejercicios.
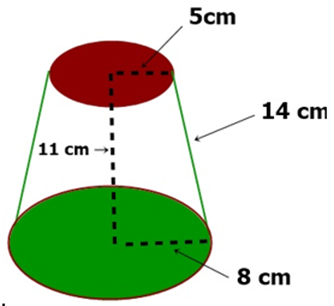
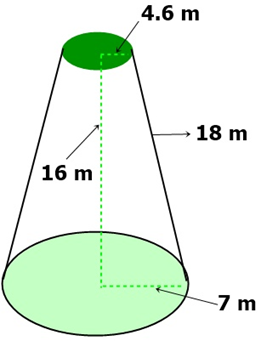
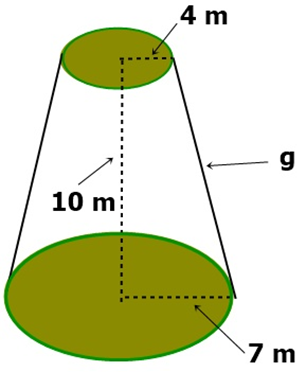
I-) Determine el área lateral en cada uno de los siguientes troncos de cono.
Entonces, la cantidad de papel que pediremos será igual a:
70.09 cm²
vídeos ejemplos.
Ejercicios.
I-) Determine el área lateral en cada uno de los siguientes troncos de cono.

II-) Analiza y resuelve los siguientes problemas.
1-) En el parque municipal de la comunidad se van a colocar baldes de basura y se tiene el siguiente modelo como se muestra en la figura. El alcalde desea saber que cantidad de material se invertirá en cada balde para su construcción. Según las medidas que se muestran a continuación. Determinar la cantidad de material que se gastará por unidad.





