Limites,Discontinuidad de funciones.

Si alguna de las tres condiciones continuidad de no se cumple, la función es discontinua en a.

La función es discontinua porque en x = 2 no existe imagen.

La función es discontinua porque en x = 2 no tiene límite.

La función es discontinua porque en x = 2 no coincide la imagen con el límite.

Continuidad en un punto

Se dice que una función f(x) es continua en un punto x = a si y sólo si se cumplen las tres condiciones siguientes:

1. Que el punto x= a tenga imagen.

2. Que exista el límite de la función en el punto x = a.

3. Que la imagen el punto coincida con el límite de la función en el punto.

Continuidad por la izquierda

Una función f(x) es continua por la izquierda en el punto x = a si:

Continuidad por la derecha

Una función f(x) es continua por la derecha en el punto x = a si:

Una función f es continua en un punto si es continua por la izquierda y es continua por la derecha:

Continuidad en un intervalo

Continuidad en un intervalo cerrado

Una función f(x) es continua en un intervalo cerrado [a, b] si:

f es continua en x, para todo x perteneciente al intervalo abierto (a, b)

f es continua en a por la derecha:

f es continua en b por la izquierda:

Consecuencia

Si f es continua en un intervalo cerrado [a, b], entonces f está acotada en dicho intervalo.

Estudiar la continuidad de 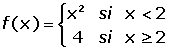en el intervalo [0, 4].

f(x) es continua por la izquierda en x = 0 , ya que f(x) = x2 por ser una función poli nómica es continua en toda .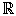

f(x) es continua por la derecha en x = 4 , ya que f(x) = 4 por ser una función poli nómica es continua en toda .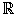

Para que f(x) sea continua en todos los puntos del intervalo (0, 4) tenemos que estudiar la continuidad en el punto x = 2, que es el único dudoso por tratarse de una función definida a trozos.

f(2)= 4

Por tanto f(x) es continua en el intervalo [0, 4].