Cálculo de Derivadas 







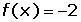
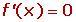


Sean a, b y k constantes (números reales) y consideremos a: u y v como
funciones.
Derivada de una constante
Derivada de x
Derivada de la función lineal
Derivada de una potencia
Derivada de una raíz cuadrada
Derivada de una raíz
Ejemplos de derivadas
1
Derivadas de sumas, productos y cocientes
Derivada de una suma
Derivada de una constante por una función
2
Derivada de un producto
Derivada de una constante partida por una función
Derivada de un cociente
Ejemplos de derivadas con operaciones de funciones
3
Derivadas exponenciales
Derivada de la función exponencial
Derivada de la función exponencial de base e
Ejemplos de derivadas exponenciales
4
Derivada de logarítmos
Derivada de un logaritmo
Como,
también se puede expresar así:
Derivada de un logaritmo neperiano
Ejemplos de derivadas de logarítmos
5
Aplicando las propiedades de los logaritmos tenemos:
Aplicando las propiedades de los logaritmos tenemos:
Derivadas trigonométricas
Derivada del seno
6
Derivada del coseno
Derivada de la tangente
Derivada de la cotangente
Derivada de la secante
Derivada de la cosecante
Ejemplos de derivadas trigonométricas
7
Derivadas trigonométricas inversas
Derivada del arcoseno
Derivada del arcocoseno
8
Derivada del arcotangente
Derivada del arcocotangente
Derivada del arcosecante
Derivada del arcocosecante
Ejemplos de derivadas trigonométricas inversas
9
Derivada de la función compuesta
Regla de la cadena
Ejemplos de derivadas de funciones compuestas
10
Derivada de la función inversa
Si f y g son funciones inversas, es decir
. Entonces
Ejemplos de derivadas de funciones inversas
Derivar, usando la derivada de la función inversa: y = arc sen x
Derivar, usando la derivada de la función inversa: y = arc tg x
Derivada de la función potencial-exponencial
Estas funciones son del tipo:
Para derivarla se puede utilizar esta fórmula:
O bien tomamos logaritmos y derivamos:
11
.







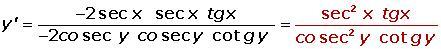



.
.
.
.
Ejemplos de derivadas de funciones potenciales-exponenciales
Derivar tomando logaritmos:
.
.
.
.
Derivadas sucesivas
Si derivamos la derivada de una función, derivada primera, obtenemos una nueva
función que se llama derivada segunda, f''(x).
Si volvemos a derivar obtenemos la derivada tercera, f'''(x).
Si derivamos otra vez obtenemos la cuarta derivada f'v y así sucesivamente.
Ejemplo:
Calcula las derivadas 1ª, 2ª, 3ª y 4ª de:
12
Derivada enésima
En algunos casos, podemos encontrar una fórmula general para cualquiera de las
derivadas sucesivas (y para todas ellas). Esta fórmula recibe el nombre de derivada
enésima, f'n(x).
Ejemplo:
Calcula la derivada enésima de:
13
Funciones implícitas
Derivación implícita
Una correspondencia o una función está definida en forma implícita cuando no
aparece despejada la y sino que la relación entre x e y viene dada por una ecuación
de dos incógnitas cuyo segundo miembro es cero.
Derivadas de funciones implícitas
Para hallar la derivada en forma implícita no es necesario despejar y. Basta
derivar miembro a miembro, utilizando las reglas vistas hasta ahora y teniendo
presente que:
x'=1.
En general y'≠1.
Por lo que omitiremos x' y dejaremos y'.
Ejemplos:
Cuando las funciones son más complejas vamos a utilizar una regla para facilitar el
cálculo:
14
Diferencial de una función
Sea f(x) una función derivable. Diferencial de una función correspondiente al
incremento h de la variable independiente, es el producto f'(x) · h. Se representa
por dy.
La diferencial en un punto representa el incremento de la ordenada de la
tangente, correspondiente a un incremento de la variable.
Ejemplo:
Calcular la diferencial de las funciones:
15
Calcular el incremento del área del cuadrado de 2 m de lado, cuando aumentamos
1mm su lado.
S = x 2dS = 2x dx
d(S)= 2·2· 0.001 = 0.004 m2
16
Función
Constante
Tabla de derivadas de funciones compuestas
Derivada Ejemplos
y=k
Identidad
y=x
y'=0
y'=1
y=8
y=x
y'=0
y'=1
Funciones potenciales
Derivadas de sumas, restas, productos y cocientes de funciones
17
Funciones exponenciales
Funciones logarítmicas
Funciones trigonométricas
18
19






Responderemos lo mas rápido posible.