Limites, Límite de una función.
Límite de una función en un punto
El límite de la función f(x) en el punto x0, es el valor al que se acercan las imágenes (las y) cuando los originales (las x) se acercan al valor x0. Es decir el valor al que tienden las imágenes cuando los originales tienden a x0.
Vamos a estudiar el límite de la función f(x) = x2 en el punto x0 = 2.
x
|
f(x)
|
1,9
|
3,61
|
1,99
|
3,9601
|
1,999
|
3,996001
|
...
|
...
|
↓
|
↓
|
2
|
4
|
x
|
f(x)
|
2,1
|
4.41
|
2,01
|
4,0401
|
2,001
|
4,004001
|
...
|
...
|
↓
|
↓
|
2
|
4
|
Tanto si nos acercamos a 2 por la izquierda o la derecha las imágenes se acercan a 4.
Se dice que la función f(x) tiene como límite el número L , cuando x tiende a x0, si fijado un número real positivo ε , mayor que cero, existe un numero positivo δ dependiente de ε , tal que, para todos los valores de x distintos de x0 que cumplen la condición |x - x0| < δ , se cumple que |f(x) - L| <ε .
También podemos definir el concepto de límite a través de entornos:
Límites laterales
Diremos que el límite de una función f(x) cuando x tiende hacia a por la izquierda es L, si y sólo si para todo ε > 0 existe δ > 0 tal que si x  (a − δ, a ) , entonces |f (x) - L| <ε .
(a − δ, a ) , entonces |f (x) - L| <ε .
Diremos que el límite de una función f(x) cuando x tiende hacia a por la derecha es L , si y sólo si para todo ε > 0 existe δ > 0 tal que si x  (a, a + δ), , entonces |f (x) - L| <ε .
(a, a + δ), , entonces |f (x) - L| <ε .
El límite de una función en un punto si existe, es único.
En este caso vemos que el límite tanto por la izquierda como por la derecha cuando x tiende a 2 es 4.
El límite de la función es 4 aunque la función no tenga imagen en x = 2.
Para calcular el límite de una función en un punto, no nos interesa lo que sucede en dicho punto sino a su alrededor.
Ejemplo
Dada la función:
Hallar 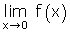 .
.
Como no coinciden los límites laterales, la función no tiene límite en x = 0.
Limites infinitos
Límite infinito
Una función f(x) tiene por límite +∞ cuando x  a, si fijado un número real positivo K>0 se verifica que f(x)>k para todos los valores próximos a a.
a, si fijado un número real positivo K>0 se verifica que f(x)>k para todos los valores próximos a a.
Límite menos infinito
Una función f(x) tiene por límite -∞ cuando x  a, si fijado un número real negativo K < 0 se verifica que f(x) < k para todos los valores próximos a a.
a, si fijado un número real negativo K < 0 se verifica que f(x) < k para todos los valores próximos a a.
Límites en el infinito
Límite cuando x tiende a infinito
Límite cuando x tiende a menos infinito

