Factorización de un polinomio
Métodos para factorizar un polinomio
Sacar factor común
Consiste en aplicar la propiedad distributiva.
a · b + a · c + a · d = a (b + c + d)
Descomponer en factores sacando factor común y hallar las raíces
1 x3 + x2 = x2 (x + 1)
La raíces son: x = 0 y x = −1
2 2x4 + 4x2 = 2x2 (x2 + 2)
Sólo tiene una raíz X = 0; ya que el polinomio, x2 + 2, no tiene ningún valor que lo anule; debido a que al estar la x al cuadrado siempre dará un número positivo, por tanto es irreducible.
3 x2 − ax − bx + ab = x (x − a) − b (x − a) = (x − a) · (x − b)
La raíces son x = a y x = b.
Igualdad notable
Diferencia de cuadrados
Una diferencia de cuadrados es igual a suma por diferencia.
a2 − b2 = (a + b) · (a − b)
Descomponer en factores y hallar las raíces
1 x2 − 4 = (x + 2) · (x − 2)
Las raíces son x = −2 y x = 2
2 x4 − 16 = (x2 + 4) · (x2 − 4) = (x + 2) · (x − 2) · (x2 + 4)
Las raíces son x = − 2 y x = 2
Trinomio cuadrado perfecto
Un trinomio cuadrado perfecto es igual a un binomio al cuadrado.
a2 ± 2 a b + b2 = (a ± b)2
Descomponer en factores los trinomio cuadrados perfectos y hallar sus raíces
La raíz es x = −3, y se dice que es una raíz doble.
La raíz es x = 2.
Trinomio de segundo grado
Para descomponer en factores el trinomio de segundo grado P(x) = ax2 + bx + c , se iguala a cero y se resuelve la ecuación de 2º grado. Si las soluciones a la ecuación son x1 y x2, el polinomio descompuesto será:
ax2 + bx + c = a · (x − x1) · (x − x2)
Descomponer en factores los trinomios de segundo grado y hallar sus raíces
Las raíces son x = 3 y x = 2.
Las raíces son x = 3 y x = − 2.
Descomponer en factores los trinomios de cuarto grado de exponentes pares y hallar sus raíces
x4 − 10x2 + 9
x2 = t
x4 − 10x2 + 9 = 0
t2 − 10t + 9 = 0
x4 − 10x2 + 9 = (x + 1) · (x − 1) · (x + 3) · (x − 3)
x4 − 2x2 − 3
x2 = t
t2 − 2t − 3 = 0
x4 − 2x2 + 3 = (x2 + 1) · (x +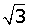 
) · (x − 
)
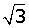Factorización de un polinomio de grado superior a dos
Utilizamos el teorema del resto y la regla de Ruffini para encontrar las raíces enteras.
Descomposición de un polinomio de grado superior a dos y cálculo de sus raíces
P(x) = 2x4 + x3 − 8x2 − x + 6
1Tomamos los divisores del término independiente: ±1, ±2, ±3.
2Aplicando el teorema del resto sabremos para que valores la división es exacta.
P(1) = 2 · 14 + 13 − 8 · 12 − 1 + 6 = 2 + 1− 8 − 1 + 6 = 0
3Dividimos por Ruffini.
4Por ser la división exacta, D = d · c .
(x − 1) · (2x3 + 3x2 − 5x − 6 )
Una raíz es x = 1.
Continuamos realizando las mismas operaciones al segundo factor.
Volvemos a probar por 1 porque el primer factor podría estar elevado al cuadrado.
P(1) = 2 · 13 + 3 · 12 − 5 · 1 − 6≠ 0
P(−1) = 2 · (− 1)3 + 3 · (− 1)2 − 5 · (− 1) − 6 = −2 + 3 + 5 − 6 = 0
(x −1) · (x +1) · (2x2 +x −6)
Otra raíz es x = −1.
El tercer factor lo podemos encontrar aplicando la ecuación de 2º grado o tal como venimos haciéndolo, aunque tiene el inconveniente de que sólo podemos encontrar raíces enteras.
El 1 lo descartamos y seguimos probando por −1.
P(−1) = 2 · (−1)2 + (−1) − 6 ≠ 0
P(2) = 2 · 22 + 2 − 6 ≠ 0
P(−2) = 2 · (−2)2 + (−2) − 6 = 2 · 4 − 2 − 6 = 0
(x − 1) · (x + 1) · (x + 2) · (2x − 3 )
Sacamos factor común 2 en último binomio y encontramos una raíz racional.
2x − 3 = 2 (x − 3/2)
La factorización del polinomio queda:
P(x) = 2x4 + x3 − 8x2 − x + 6 = 2 (x −1) · (x +1) · (x +2) · (x − 3/2)
Las raíces son : x = 1, x = − 1, x = −2 y x = 3/2
Todas las raíces son racionales
Puede suceder que el polinomio no tenga raíces enteras y sólo tenga raíces racionales.
En este caso tomamos los divisores del término independiente dividido entre los divisores del término con mayor grado, y aplicamos el teorema del resto y la regla de Ruffini.
P(x) = 12x3 + 8x2 − 3x− 2
Probamos por: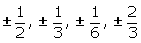 
.
Sacamos factor común 12 en el tercer factor.
Binomio al cuadrado
(a ± b)2 = a2 ± 2 · a · b + b2
(x + 3)2 = x 2 + 2 · x ·3 + 32 = x 2 + 6 x + 9
(2x − 3)2 = (2x)2 − 2 · 2x · 3 + 32 = 4x2 − 12 x + 9
Suma por diferencia
(a + b) · (a − b) = a2 − b2
(2x + 5) · (2x - 5) = (2x)2 − 52 = 4x2 − 25
Binomio al cubo
(a ± b)3 = a3 ± 3 · a2 · b + 3 · a · b2 ± b3
(x + 3)3 = x3 + 3 · x2 · 3 + 3 · x · 32 + 33 =
= x 3 + 9x2 + 27x + 27
(2x − 3)3 = (2x)3 − 3 · (2x)2 ·3 + 3 · 2x · 32 − 33 =
= 8x 3 − 36x2 + 54x − 27
Trinomio al cuadrado
(a + b + c)2 = a2 + b2 + c2 + 2 · a · b + 2 · a · c + 2 · b · c
(x2 − x + 1)2 =
= (x2)2 + (−x)2 + 12 + 2 · x2 · (−x) + 2 x2 · 1 + 2 · (−x) · 1=
= x4 + x2 + 1 − 2x3 + 2x2 − 2x=
= x4− 2x3 + 3x2 − 2x + 1
Suma de cubos
a3 + b3 = (a + b) · (a2 − ab + b2)
8x3 + 27 = (2x + 3) (4x2 − 6x + 9)
Diferencia de cubos
a3 − b3 = (a − b) · (a2 + ab + b2)
8x3 − 27 = (2x − 3) (4x2 + 6x + 9)
Producto de dos binomios que tienen un término común
(x + a) (x + b) = x2 + (a + b) x + ab
(x + 2) (x + 3) =
= x2 + (2 + 3) · x + 2 · 3 =
= x2 + 5x + 6
